vcfR documentation

by
Brian J. Knaus and Niklaus J. Grünwald

A fundamental question to most population studies is whether populations are diverse and whether this diversity is shared among the populations? To address the question of within population diversity geneticists typically report heterozygosity. This is the probability that two alleles randomly chosen from a population will be different. Ecologists may know this as Simpson’s Index (Simpson 1949). To address differentiation population geneticists typically utilize \(F_{ST}\) or one of its analogues. Population differentiation measured by \(F_{ST}\) was originally proposed by Sewall Wright (Wright 1949). This was later extended to a method based of diversity by Masatoshi Nei (Nei 1973). As researchers applied these metrics to microsatellites, genetic markers with a large number of alleles, it became clear that Nei’s measure would not correctly range from zero to one, so Philip Hedrick proposed a correction (Hedrick 2005). More recently, Lou Jost proposed another alternative (Jost 2008). You can tell a topic is popular when so many variants of it are generated. And there are more variants than I’ve mentioned here. A nice discussion as to which measure may be appropriate for your data was posted to the Molecular Ecologist blog titled should I use \(F_{ST}\), \(G_{ST}\) or \(D\)?.

In vcfR I’ve implemented the function genetic_diff() to measure population diversity and differentiation. Because VCF data typically do not include population information we’ll have to supply it as a factor. The method ‘nei’ employed here is based on the methods reported by Hedrick (Hedrick 2005). The exception is that the heterozygosities are weighted by the number of alleles observed in each population. This was inspired by hierfstat::pairwise.fst() which uses the number of individuals observed in each population to weight the heterozygosities. By using the number of alleles observed instead of the number of individuals we remove an assumption about how many alleles each individual may contribute. That is, we should be able to accomodate samples of mixed ploidy.

library(vcfR)
data(vcfR_example)
pop <- as.factor(c("us", "eu", "us", "af", "eu", "us", "mx", "eu", "eu", "sa", "mx", "sa", "us", "sa", "Pmir", "us", "eu", "eu"))
myDiff <- genetic_diff(vcf, pops = pop, method = 'nei')
knitr::kable(head(myDiff[,1:15]))
CHROM POS Hs_af Hs_eu Hs_mx Hs_Pmir Hs_sa Hs_us Ht n_af n_eu n_mx n_Pmir n_sa n_us
Supercontig_1.50 2 0 0.0 0.000 0.5 0.000 0.00 0.0798611 2 4 4 2 4 8
Supercontig_1.50 246 NaN 0.0 0.375 NaN 0.000 0.50 0.3512397 0 4 4 0 6 8
Supercontig_1.50 549 NaN 0.0 NaN NaN NaN 0.50 0.4444444 0 2 0 0 0 4
Supercontig_1.50 668 NaN 0.5 0.000 NaN 0.000 0.50 0.5000000 0 4 2 0 2 8
Supercontig_1.50 765 0 0.0 0.000 0.0 0.000 0.00 0.1107266 2 12 4 2 4 10
Supercontig_1.50 780 0 0.0 0.000 0.0 0.375 0.18 0.1244444 2 8 4 2 4 10

The function returns the chromosome and position of each variant as provided in the VCF data. This should allow you to align its output with the VCF data. The heterozygosities for each population are reported as well as the total heterozygosity, followed by the number of alleles observed in each population. Note that in some populations zero alleles were observed. Populations with zero alleles reported heterozygosities of ‘NaN’ because of this absence of data.

knitr::kable(head(myDiff[,16:19]))
Gst Htmax Gstmax Gprimest
0.4782609 0.7951389 0.9475983 0.5047085
NaN 0.8057851 NaN NaN
NaN 0.6666667 NaN NaN
NaN 0.8125000 NaN NaN
1.0000000 0.7543253 1.0000000 1.0000000
0.1160714 0.8000000 0.8625000 0.1345756

The remaining columns contain \(G_{ST}\), the maximum heterozygosity, the maximum \(G_{ST}\) and finally \(G'_{ST}\). The maximum heterozygosity and the maximum \(G_{ST}\) are intermediary values used to calculate \(G'_{ST}\). They are typically not reported but provide values to help validate that \(G'_{ST}\) was calculated correctly. Note that the populations that had zero alleles and therefore a heterozygosity of ‘NaN’ contributed to \(G_{ST}\)s that were also ‘NaN’. To avoid this you may want to consider omitting populations with a small sample size or that contain a large amount of missing data.

We now have information for each variant in the VCF data. Because this is typically a large quantity of information, we’ll want to summarize it. One way is to take averages of the data.

knitr::kable(round(colMeans(myDiff[,c(3:9,16,19)], na.rm = TRUE), digits = 3))
x
Hs_af 0.176
Hs_eu 0.188
Hs_mx 0.168
Hs_Pmir 0.052
Hs_sa 0.198
Hs_us 0.155
Ht 0.247
Gst 0.595
Gprimest 0.632

Another way to summarize data is to use violin plots.

library(reshape2)
library(ggplot2)

dpf <- melt(myDiff[,c(3:8,19)], varnames=c('Index', 'Sample'), value.name = 'Depth', na.rm=TRUE)
## No id variables; using all as measure variables
p <- ggplot(dpf, aes(x=variable, y=Depth)) + geom_violin(fill="#2ca25f", adjust = 1.2)
p <- p + xlab("")
p <- p + ylab("")
p <- p + theme_bw()
p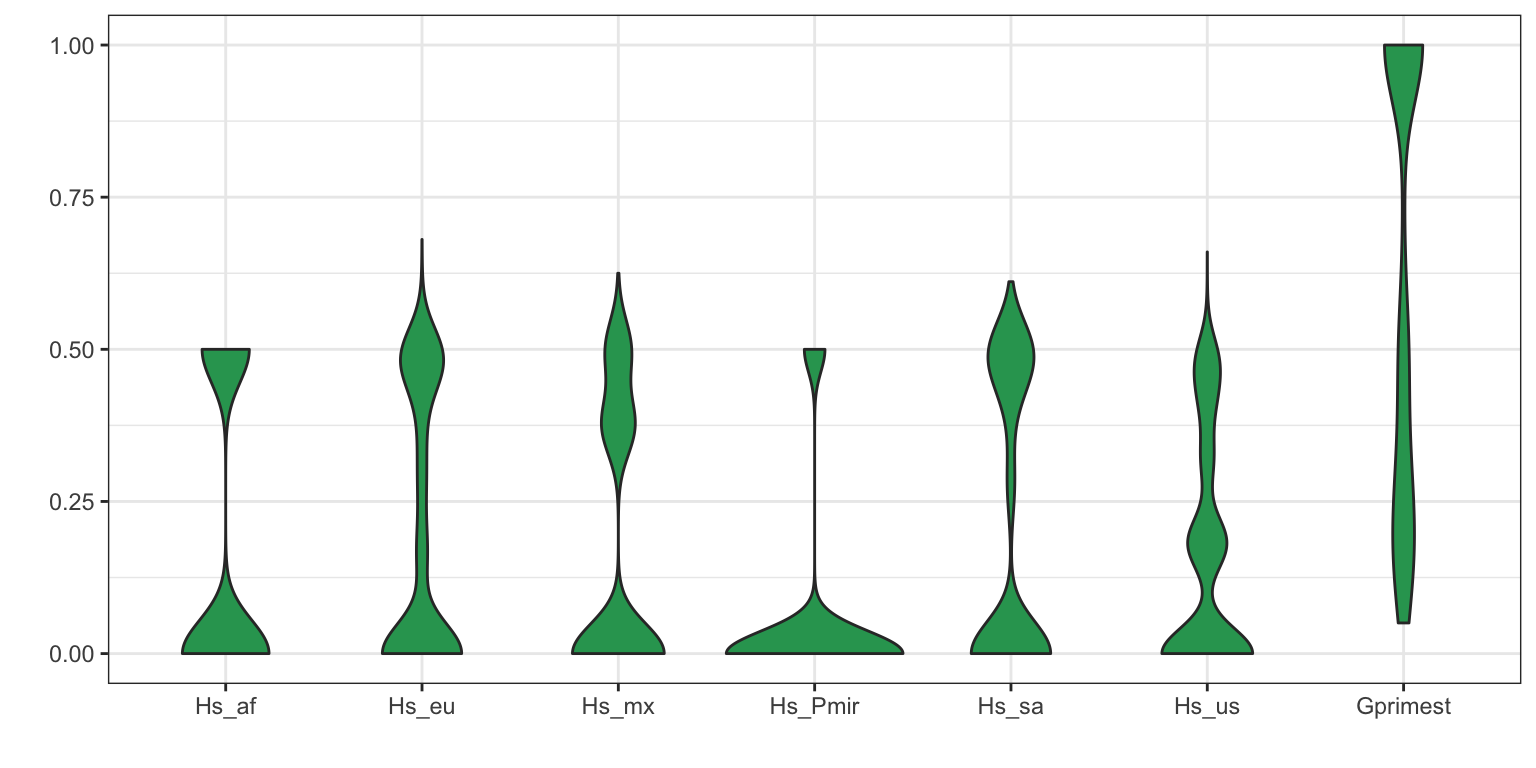

References

Hedrick, Philip W. 2005. “A Standardized Genetic Differentiation Measure.” Evolution 59 (8): 1633–38.
Jost, Lou. 2008. “GST and Its Relatives Do Not Measure Differentiation.” Molecular Ecology 17 (18): 4015–26.
Nei, Masatoshi. 1973. “Analysis of Gene Diversity in Subdivided Populations.” Proceedings of the National Academy of Sciences 70 (12): 3321–23.
Simpson, Edward H. 1949. “Measurement of Diversity.” Nature 163: 688.
Wright, Sewall. 1949. “The Genetical Structure of Populations.” Annals of Eugenics 15 (1): 323–54.

Copyright © 2017, 2018 Brian J. Knaus. All rights reserved.

USDA Agricultural Research Service, Horticultural Crops Research Lab.